Ça alors.. 19+ Listes de Standard Deviation Normal Distribution! A normal distribution has some interesting properties:
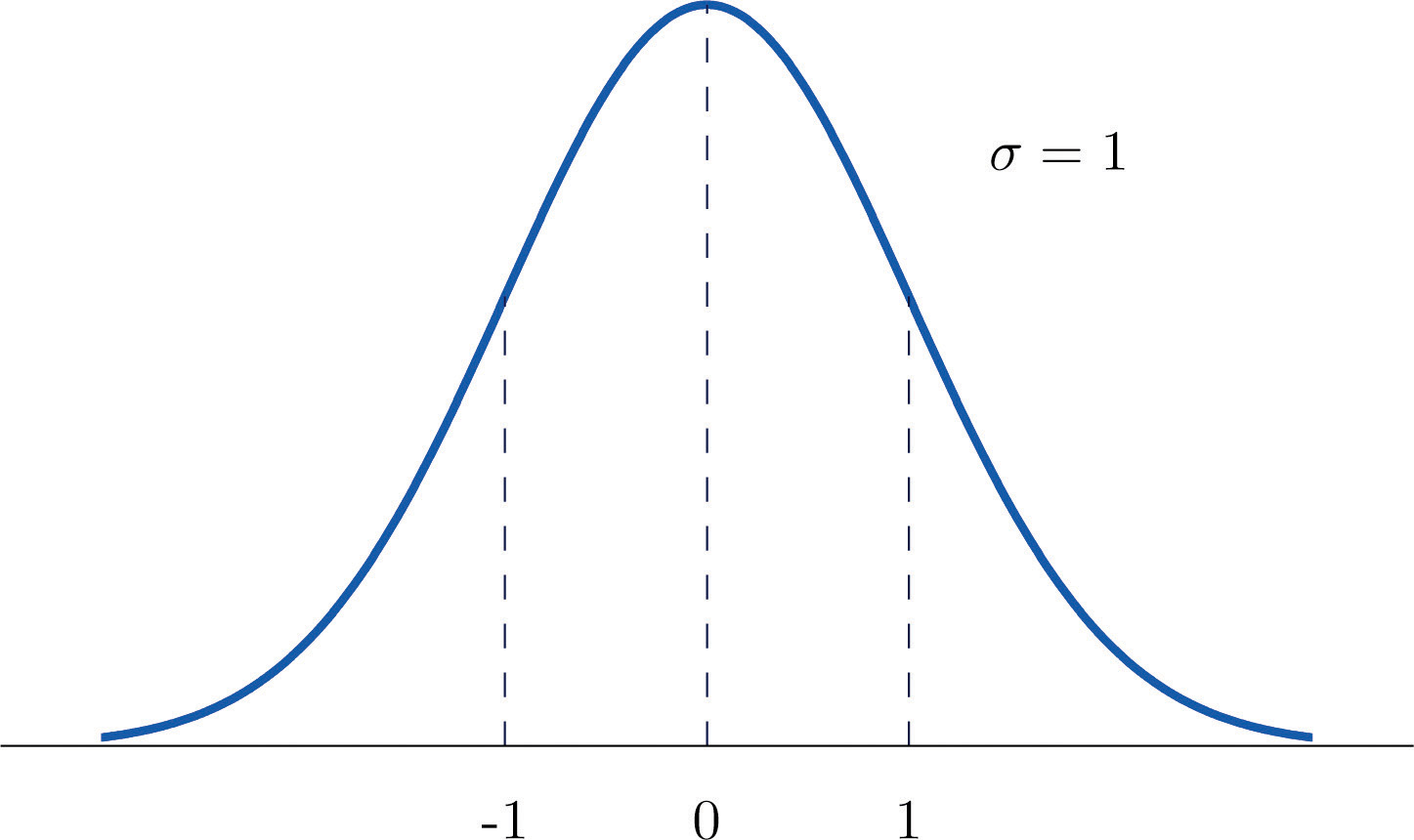
Standard Deviation Normal Distribution | The standard deviation is 1. Produces the distribution z ~ n(0, 1). Σ is the standard deviation (std) value. Standard deviation is one of the most powerful tools in statistics, especially when it comes to normal distributions. In the standard normal distribution, the mean and standard deviation are always fixed.
The distribution is spread symmetrically around the central location which happens when occurrences are equally above and below an average. Σ has a standard normal distribution. A normal distribution has some interesting properties: Produces the distribution z ~ n(0, 1). The standard normal distribution is a normal distribution with mean μ = 0 and standard deviation σ = 1.

A normal distribution exhibits the following: A normal distribution has some interesting properties: Distributes as the standard normal distribution, so you can calculate any normal distribution based on the standard normal distribution. It is also called gaussian distribution because it was first discovered by carl friedrich gauss. 68.3% of the population is contained within 1 standard deviation from the mean. How to use standard normal table. The normal distribution is the most common probability distribution in statistics. Here is the standard normal distribution with percentages for every half of a standard deviation , and cumulative percentages use the standard normal distribution table when you want more accurate values. The standard deviation is 1. Question 1 question 2 question 3 question 4 question 5 question 6 question 7. It is for this reason that it is included among the lifetime distributions commonly used for reliability and life data analysis. A normal distribution with mean of zero and standard deviation of one. Problems and applications on normal distributions are presented.
A radar unit is used to measure speeds of cars on a motorway. The normal distribution is a probability distribution. Everything you want to know about the normal distribution: Problems and applications on normal distributions are presented. The speeds are normally distributed with a mean of 90 km/hr and a standard deviation of 10 km/hr.
Practice problems for normal distribution. Everything you want to know about the normal distribution: Σ is the standard deviation (std) value. I generated samples from normal then transformed them into lognormal distribution. While the mean indicates the central or average value of the entire dataset, the standard deviation indicates the spread or variation of. Produces the distribution z ~ n(0, 1). A normal distribution exhibits the following: It is also called gaussian distribution because it was first discovered by carl friedrich gauss. Normal distributions come up time and time again in statistics. Standard normal distribution table is used to find the area under the f(z) function in order to find the probability of a specified range of distribution. It is denoted as $n(0,1)$. The mean, mode and median are all 0. In this case, the probability density moreover, these tests work well even if the distribution is approximately normally distributed.
The standard deviation is 1. In the standard normal distribution, the mean and standard deviation are always fixed. It is denoted as $n(0,1)$. Histogram of the vehicle weight variable with a superimposed curve. The following two videos give a description of what it means to have a data set that is normally distributed.
The solutions to these problems are at the bottom of the page. Normal distribution mean and standard deviation.in this video i show you how to find the mean and standard deviation for a normal distribution given two. The distribution function of a normal random variable can be written as where is the distribution function of a standard normal random variable by increasing the standard deviation from to , the location of the graph does not change (it remains centered at ), but the shape of the graph changes. Firstly, i am using mu and sigma as parameters in rnorm(), then i mean and standard deviation are specified in log scale. The standard normal distribution has a fixed set of values. Its mean the standard normal distribution is the normal distribution with mean 0 and standard deviation 1. If a variable x has. Normal distributions have the following features example 1: Standard normal distribution table is used to find the area under the f(z) function in order to find the probability of a specified range of distribution. It is denoted as $n(0,1)$. The standard normal distribution is the normal distribution with mean 0 and standard deviation 1. The mean, mode and median are all 0. While the mean indicates the central or average value of the entire dataset, the standard deviation indicates the spread or variation of.
The distribution is spread symmetrically around the central location which happens when occurrences are equally above and below an average standard deviation. The standard normal distribution has a fixed set of values.
Standard Deviation Normal Distribution: The letter z is often used to denote a the standard normal distribution can represent any normal distribution, provided you think in terms of the number of standard deviations above or.